Symmetry-breaking motion of a magnet: spin revolution
Any rotation changes the trajectory of an object. Particularly, a spinning object acts as a gyroscope moving perpendicularly to the applied force ({mathbf{F}}_{{{text{appl}}}}) and obeying the dynamics of the gyroscope axis ({{varvec{uprho}}}): (frac{{partial {{varvec{uprho}}}}}{partial t} = frac{{R^{2} }}{{I_{{text{cm}}} omega }}({mathbf{L}}_{rho } times {mathbf{F}}_{{{text{appl}}}} ))fifteen. There is, however, an important distinction between a standard gyroscope and a revolving magnet described here: the revolution axis is magnetic. The equation of motion becomes (with (gamma) being the gyromagnetic ratio):
$$partial {mathbf{M}}_{{{text{eq}}}} /partial t = frac{{gamma R^{2} }}{{I_{{text{cm }}} Omega_{{text{R}}} }}({mathbf{L}}_{{text{R}}} times {mathbf{F}}_{{{text{ appl}}}} )$$
(4)
This outcome contains interesting physics. First, a magnetic sphere on an incline should revolve up spontaneously, without any external torque around Mek that is different from ({{varvec{uptau}}}_{{text{B}}}), ({{varvec{uptau}}}_{{{text{Fs}}}}) as well as their sum. Second, the time-reversal symmetry becomes broken as an action of the time operator T on the left side of Eq. (4) (frac{{T({mathbf{M}}_{{{text{eq}}}} )}}{T
(5)
Interestingly, it depends neither on (theta_{{{text{eq}}}}) nor on the mass m. Generally, ({mathbf{v}}_{{text{R}}} ne {mathbf{v}}) (Fig. 2f) and can be found numerically by deriving Mek from Eq. (2), inserting the result into Eq. (1), and solving Eqs. (1)–(4).
Figure 3b shows ({{varvec{Omega}}}_{{text{R}}}) of a NdFeB sphere in three cases: Yo corresponding to the set-up of Fig. 3a with linear velocity ({mathbf{v}} = 5) m/s; II corresponding to the rolling down an incline with (beta = pi /10) and ({mathbf{B}} = ( – 0.95, – 0.22,0.22)10^{ – 5}) T; and III corresponding to the rolling down an incline with (beta = pi /10) and ({mathbf{B}} = (0,1,0)10^{ – 5}) T. As one can see from this data ({{varvec{Omega}}}_{{text{R}}}) can be varied in a broad range by changing the applied force or inclination.
Spin revolution effect in a system of two hard magnets
Now we switch to the SR in time-dependent fields. Let us consider two magnetic spheres, each put into a vertical non-magnetic tube. The tubes are placed close to one another and the spheres arrange themselves on internal sides of the tubes due to the magnetic attraction ({mathbf{F}}_{{text{m}}}^{12}) and ({mathbf{F}}_{{text{m}}}^{21})10 as shown in Fig. 3c,d. If the tubes are rotated about their vertical axes due to ({mathbf{F}}_{{{text{appl}}}}), the spheres rotate initially together with the tubes. At a critical angle (beta)the sum of gravitational and magnetic forces overcomes the frictional force Fs and the spheres move upwards against intuitive expectation that they return to their initial or to somewhat lower positions in response to ({mathbf{F}}_{{text{m}}} + m{mathbf{g}}). The reason for this counterintuitive behavior is the SR emerging at a critical angle (beta)when the net torque ({mathbf{T}}_{{text{cm}}}) vanishes. According to Eq. (4) the Mek (and spheres) should move upwards for any ({mathbf{F}}_{{{text{appl}}}}). Our experiments support the expectation of emerging revolution as well as that of a lifting force defying gravity which tries to push the spheres downwards, and the magnetic interaction attracting the spheres in horizontal direction (see Fig. 3c and Movie S58).
In time-reversal invariant systems, the equations of motion are invariant under the transformation (({mathbf{q}},{mathbf{p}},t) mapsto^{T} ({mathbf{q}}, -{mathbf{p}}, -t)) with what being the coordinates, p the momentum and you the time. In other words, the trajectory in reversed time should be a backward sequence of positions constituting the trajectory in forward time.16,17. To check this, one reverses the momentum p and looks for the corresponding trajectory. If one reverses the rotational momentum of the tubes, the spheres will not go downwards. They will repeatedly move upwards to any tube height (Fig. 4, Movie S58) breaking the time-reversal symmetry. Importantly, this symmetry breaking is neither local, like that of a Lorentz force, nor dissipation-driven. Indeed, the trajectory of a charge due to the Lorentz force becomes time-reversal invariant if the direction of magnetic field is reversed, because ({mathbf{B}} mapsto^{T} – {mathbf{B}}) (see8part D and Fig. S18). The only way to force the spheres moving downwards is to reverse the gravitational force. This operation is, however, forbidden as the forces are even under time-reversal (({mathbf{F}} mapsto^{T} {mathbf{F}})).
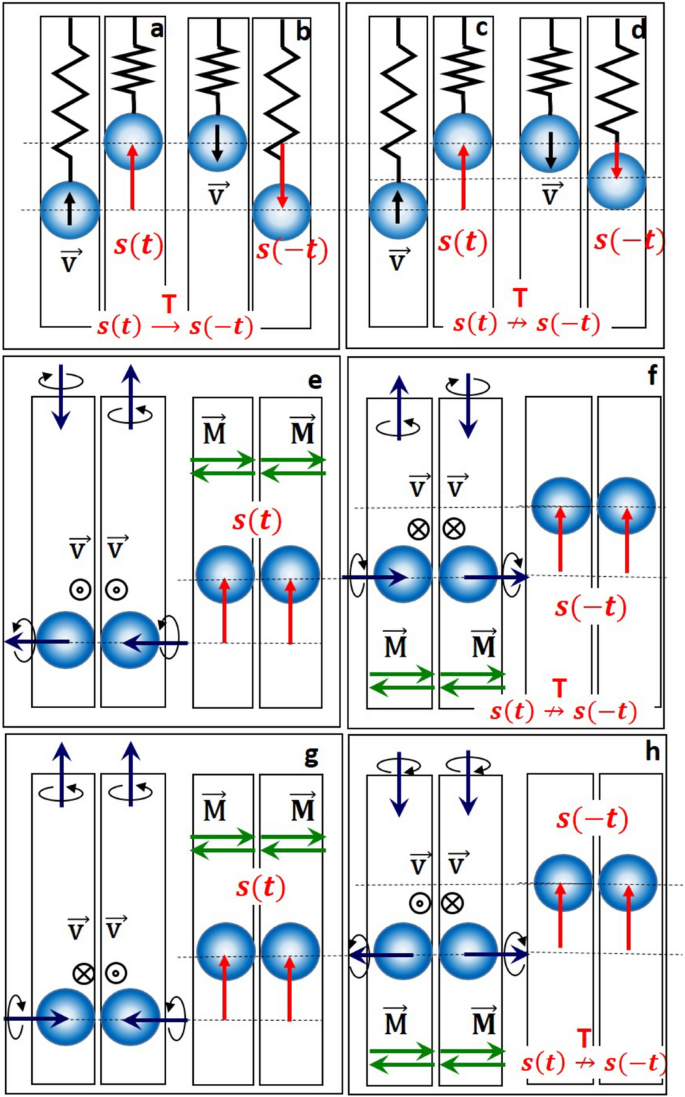
Time-reversal symmetry breaking. (a,b) Side-view of the forward-in-time ((s